CS231n 4. Introduction to Neural Networks (요약,정리!)

Backpropagation (gradient for neural network)

네트워크 전체에 대해 Chain rule(연쇄 법칙)을 적용하여 gradient를 계산하는 방법 중 하나로 이를 이용해 loss function의 gradient를 구해 parameter들을 최적화(optimization)하는데 사용한다. 또한 neural networks을 효과적으로 개발, 디자인 및 디버그하는데 중요하다

우리가 Backpropagation를 공부하는 이유?

실제로 #analytic_gradient 를 어떻게 계산하는지에 대해 알아볼거임!
여러개의 linear classification을 사용할 경우 gradient를 어떻게 찾을 것인지!=> 이 gradient를 이용해 loss를 구함
    - 입력값 xi(이미지)에 대해 gradient 계산이 쉬울지라도 실제로는 parameter(W)에 대한 gradient는 주로 계산
    - 이 gradient 값을 토대로 다시 parameter(W)를 업데이트 함
    - 후에 neural network가 어떻게 작동,해석,시각화하는지에 대해 xi의 gradient에 따라 활용될 수 있음
      => backpropagation(역전파)이 필요하다!
[[CS231n 3. Linear Classification (Optimization)]]

Interpretation of gradient & Computational graph

미분은 각 변수가 해당값에서 전체함수의 결과값에 영향을 미치는 민감도라고 볼 수 있다!

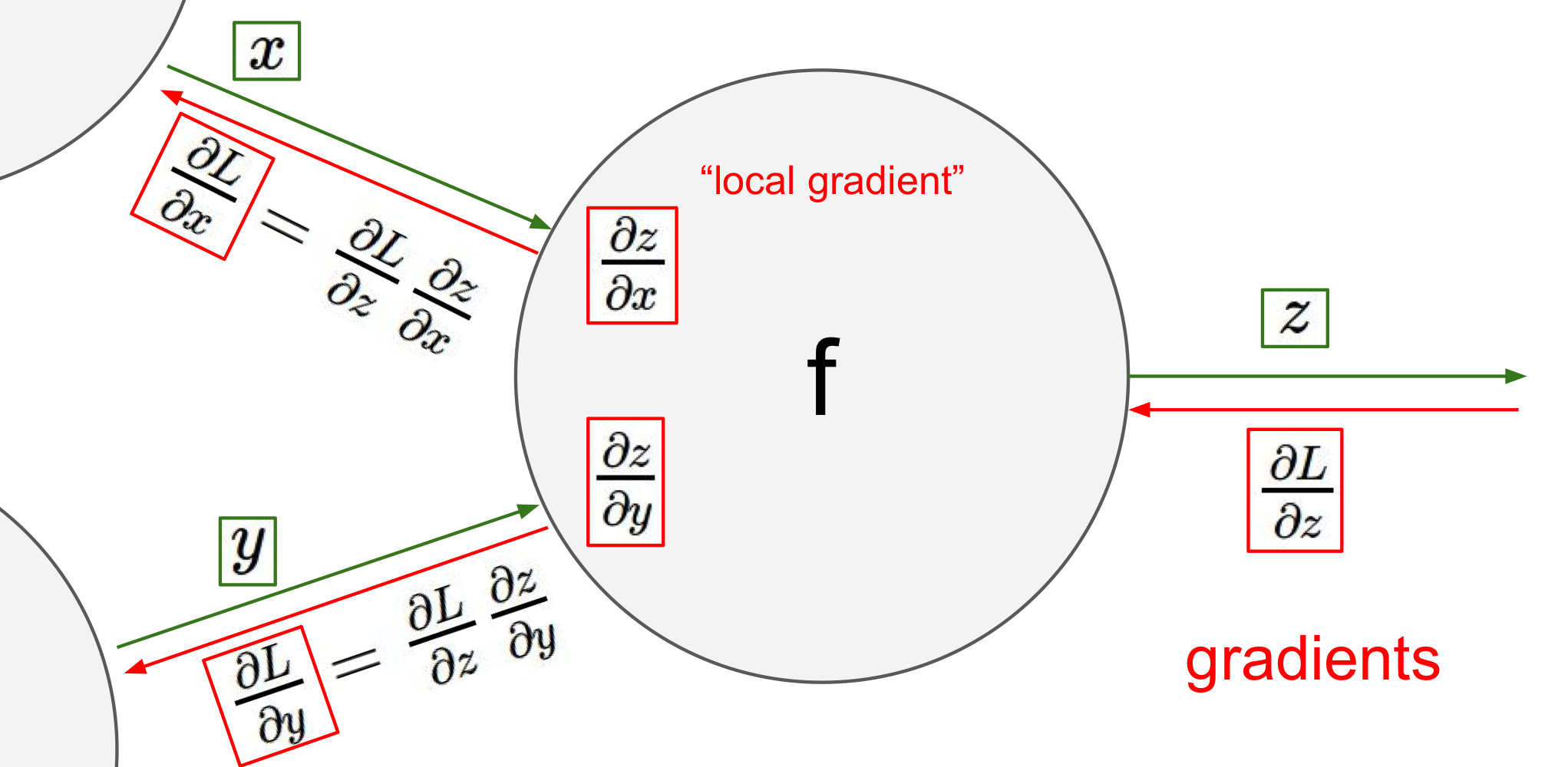
Computational Graph: 밑에 사진이 이 예시로 사람들이 이해하기 쉽도록 만든 그래프이다
    - input value & local gradient 값을 쉽게 파악 가능
    - 복잡한 형태의 anaytic gradient 쉽게 계산 가능

computational graph

 

 

Backpropagation 과정

gradient를 얻기위한 chain rule에 순서에 대해서 설명하고 있다

1. 함수에 대한 computational graph 만들기
   • 변수와 계산가능한(미분가능한) 연산을 미리 만들어 node를 만들어놓음
   • 미분 가능한 연산부분(gate)에서 local gradient를 구해놓아야함
2. 각 local gradient 구해놓기
3. chain rule를 이용해서 식을 정리하기
4. z에 대한 최종 loss L은 이미 계산되어 있기 때문에 output layer에서 backpropagation 시작
5. 최종 목적지는 input에 대한 gradient를 구하는것 (뒤로 오면서 gradient를 계속 계산)

Gate에서의 Backpropagation 동작

 

 

 

 

Example 1) 기초

f(x,y,z)=(x+y)z, 변수는 x,y,z/ 미분 가능한 연산은 +와 X(곱하기)

1. computational graph 그리기: 변수에서 시작/ 미분 가능한 연산에서 합쳐짐
2. local gradient 구하기: dq/dx=1, dq/dy=1, df/dq=z, df/dz=q
3. chain rule: df/dy=df/dq X dq/dy=(-4)X1=-4

이 부분에서 알 수 있는 것은 x와 y는 현재 음의 gradient를 가지고 있는데 이는 곧 4의 힘으로 낮아지기를 원한다고 볼 수 있음

• 만약 x,y가 음의 gradient이기 때문에 이에 대한 반응으로 감소하면 덧셈gate 출력이 감소
• 덧셈게이트 출력이 감소하면 곱셈게이트 출력이 증가

=> backpropagation은 보다 큰 최종 출력값을 얻도록 게이트들이 자신들의 출력을 얼마나 강하게 증가/감소하길 원하는지 소통하는 과정이라고 볼 수 있다.

 

 

 

 

Example 2) Sigmoid

이를 통해 알 수 있는 점은 위에 #sigmoid 예제처럼 간단한 형태로 미분 가능한 식을 알고 있다면 연산 gate를 여러가지로 만들필요 없이 하나로 줄일 수 있다는 것이다.

Input gradient=[local gradient]X[upstream gradient]

• local gradient: 미리 구해둔 도함수에 x(input: 함수값)값을 넣어서 얻은 값
• upstream gradient: 앞쪽 gate에서 받거나 얻은 gradient 값으로 상수가 된다.

 

 

Example 3) Input이 vector일 경우

이 경우에는 input이 더 이상 상수가 아니라 input이 vector일 경우로 이럴 때는 #jacobian 으로 계산하면 됨

백터의 gradient는 항상 원본 백터의 사이즈와 같다는 것을 유의하여 검산시에 참고해야함! 선형함수로 행렬들이 서로 곱해져 결국에는 하나의 행렬이 되어 score도 선형함수가 됨

 

 

 

Setting Up Architecture (Neural Network)

Linear Classification의 문제점:

[!] 비선형성이 매우 중요함!

• 중간에 layer을 추가해서 더 복잡한 패턴이 학습 가능함
• 기존에는 s=Wx꼴(linear), 하지만 이제는 #backpropagation 을 통해 여러가지 layer을 거쳐 parameter을 학습시키고 score을 계산하여 구하기 때문!

 

 

Neural Network 형태 및 구조: 

앞쪽 layer의 axon에서 보낸 정보(x0)를 synapse(w0: 고유의 값으로 학습 가능함=synaptic strengths)를 통해 받아 dendrite가 이 정보와 강도를 곱해 (x0w0) cell body로 가져오고 activation function을 통해 다음 layer로 이동을 한다. 이때 activation function에는 여러가지가 있으며 Neural Network 구조에는 크게 fully connected layer과 CNN이 있음

 

Modeling one Neuron

생물학(뇌)와의 연관성

• neuron: like와 dislike를 할 수 있는 능력이 있음
• dendrite: 정보를 받아들이는 역할(수용체)
• synapse: 뉴런들간의 신호가 전달되는 부분 => 강도와 효율성이 있음
• cell body: 모든 정보를 모음
• axon: 정보를 내보내는 역할실제 computational 모델

1. 앞쪽 layer의 axon에서 보낸 정보(x0)를 synapse(w0: 고유의 값으로 학습 가능함=synaptic strengths)를 통해 받아 dendrite가 이 정보와 강도를 곱해 (x0w0) cell body로 가져오게 됨
2. cell body로 오게 된 정보(x0w0)는 #activation_function 을 만나 뉴런의 firing rate 를 model함
   • 오직 firing의 빈도수(frequency)만이 communicate하는데 정보로 활용이 됨
3. activaition function을 지나고 나온 정보는 다시 axon을 거쳐 다음 neuron, 즉 다음 layer로 넘어감

activation function: 비선형함수로 사용되며 입력 신호의 가중치의 합을 반환한다. 이때  발화의 빈도에 대해 부호를 해석하여 (시그모이드에서 음수면 가만히 있음) 뉴런의 발화빈도를 f로 모델링한다.

물론 실제뇌는 매우 복잡해서 정밀한 비교를 하기 어려움
Neuron은 like와 dislike를 할 수 있는 능력이 있음 => single neuron을 linear classifier로 볼 수 있음
- Binary Softmax classifier, Binary SVM classifier, Regularization(like, dislike여서 binary인듯)

 

 

 

 

Activation Function

Activation function에는 크게 #sigmoid 와 #ReLU function이 존재한다
Sigmoid:
모든 정수값을 가지고 값의 범위를 0~1 사이로 압축시킴 (0: 아예 firing 안함, 1: 완전한 firing)
    -  단점1. kill gradient: 함수 값이 0과 1에 근사할 경우 gradient가 0이되어 local gradient가 매우 작아져 backpropagation을 하며 gradient를 0으로 만들어 kill할 수 있음
    - 단점 2. not zero-centered: 함수값이 0을 중심으로 있지 않기 때문에 값이 역동적으로 바뀌지 않으며 계속 양수값이거나 음수값이 됨 (처음 시작에 모든걸 결정)

 

 

ReLU (Recified Linear Unit): f(x)=max(0,x)
    - 장점 1. accerlate 계산속도: 함수가 linear function이기 때문에 gradient를 계산하고 적용하는데 매우 빠름
    - 장점 2. 0을 기준으로 한 임계값에 적용이 가능함
    - 장점 3. gradient가 극값으로 가도 값이 일정하여 kill되지 않음
    - 단점 1. training 동안 die 가능: 음수값을 가지게 되면 함수값이 0이 되어 다시 살아나지 못함

 

Neural Network architectures

1. Fully connected layer
   acyclic loop로 두개의 인접한 layer의 모든 뉴런들끼리 완전히 연결되어있는 형태 (fully pairwise)
   단, 같은 layer 내에서는 연결이 되어있지 않다

• Naming 규칙: input layer은 N-layer에서 N에 들어가지 않으며 총 3가지 layer(input, hidden, output)은 2-layer Neural Network로 불림
• Outer layer: activation function을 가지고 있지 않고 class score을 나타내는데 사용됨
• Parameter의 개수 ~ neuron의 개수 + Weight의 개수 + bias의 개수
  => 이를 통해 neural network의 크기를 측정함

2. [[CS231n 5. Convolutional Neural Network (CNN)]]